알고리즘 문제 푸는데 위치관계에 대한 이해가 필요한 것 같아 포스팅한다.
공부하는 겸... 아 정말이지 세상 쉬운거 하나 없다 이럴 때 후회되는 건 어릴 때 수학공부나 열심히 해둘 걸... 하지만 지금 후회해봤자 무슨 소용인가 지금 열심히 할 수 밖에 없는 듯...

두 원의 위치관계
원과 원의 사이의 거리는 두 원의 중심사이의 거리(중심거리)를 이용하고, 두 원의 반지름은 모두 이용한다.
정확히 말하면 반지름의 합과 차를 이용한다는 것이다.
두 원을 각각 O, O'이라고 해보자.
그리고 원 O의 반지름을 r, 원 O'의 반지름을 r', 두 원의 중심사이의 거리를 d라고 해보자.
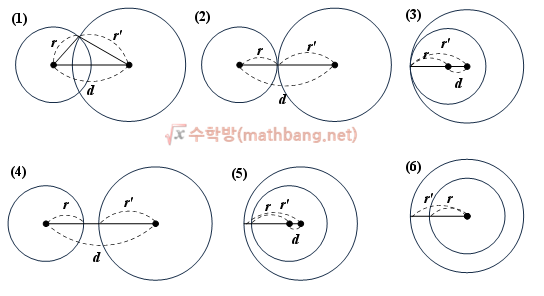
두 원의 위치관계 - 두 점에서 만나는 경우
첫 번째로 두 원이 두 점에서 만나는 경우가 있다. 원이 두 점에서 만난다는 얘기는 서로 겹친다는 것이다.
두 원이 서로 겹치려면 작은 원의 반지름보다 가까운 거리에서 만나야 한다.
그래서 두 원의 반지름을 더한 값이 중심거리보다 커야 한다. r+r' > d가 되어야 한다는 말이다.
그럼 r+r' > d만 되면 될까?
(5)번 그림을 보자. (5)번은 r+r' > d이다. 그런ㄹ데 두 점에서 만나지 않는다. 따라서 두 점에서 만나는 경우에는 r+r' > d 말고 다른 조건이 또 필요하다.
어떤 조건이냐면 r' - r < d라는 조건이다.
큰 원의 반지름에서 작은 원의 반지름을 뺀 것이 중심거리보다 작아야 한다는 이야기다.
결과적으로 두 원이 두 점에서 만나려면 r' - r < d < r+ r'가 되어야 한다.
두 원의 위치관계 - 한 점에서 만나는 경우, 내접, 외접
두 번째는 두 원이 한 점에서 만나는 경우다. 한 점에서 만나는 경우는 두 가지가 있는데, 하나는 (2)번처럼 작은 원이 큰 원의 바깥에 있으면서 한 점에서 만나는 경우가 있다.
이 대는 두 원의 반지름을 더한 것이 주심거리와 같은 r + r' = d가 되어야 한다.
이 때를 서로 바깥에서 만난다고 해서 외접이라고 한다.
다른 경우는 (3)번처럼 작은 원이 큰 원의 안쪽에 들어 있으면서 한 점에서 만나는 경우다.
이 때는 큰 원의 반지름에서 작은 원의 반지름을 뺀 것이 중심거리와 같아야 한다.
즉, r' - r = d가 되어야 한다.
이때는 큰 원의 안에서 만난다고 해서 내접이라고 한다.
두 원의 위치관계 - 만나지 않는 경우, 외부에 있을 때, 내부에 있을 때, 동심원
세 번째는 만나지 않는 경우다. 만나지 않는 경우는 세 가지가 있다.
(4)번처럼 두 원이 완전히 떨어져서 만나지 않는 경우다.
이 때는 두 원의 반지름의 합보다 중심거리가 더 길어야 된다. r + r' < d 이다.
(5)번은 작은 원이 큰 원의 안에 있으면서 서로 만나지 않는 경우다. (3)번과 다르다.
이 때는 큰 원의 반지름에서 작은 원의 반지름을 뺀 것이 중심거리보다 커야 한다. d < r' - r이다.
(6)번은 아주 특이한 경우인데, 두 원의 중심이 같고 반지름이 다른 경우다.
두 원의 중심이 같으니까 중심거리가 0이다. d = 0, r ≠ r' 인 경우다.
두 원의 위치관계에서는 특별히 얘기하지 않으면 두 원의 반지름이 다른 것으로 보기 때문에 d = 0만 써도 크게 상관은 없다. 이처럼 중심이 같고, 반지름이 다른 원을 동심원이라고 한다.
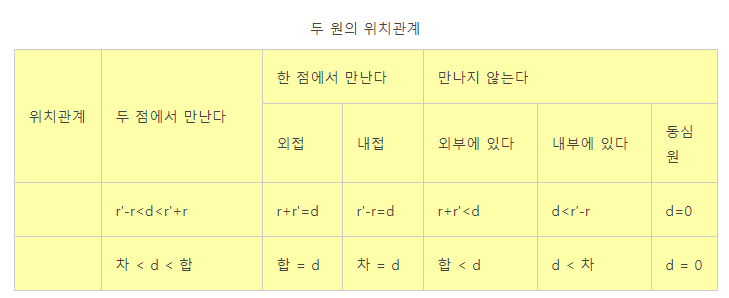
두 원의 위치관계 찾기
두 원의 위치관계를 알고 싶을 때는 두 원의 반지름의 합과 차를 미리 구하자.
그리고 중심거리가 합과 차의 사이에서 어디에 있는지 보면 된다.
만약 중심거리가 차보다 작으면 내부에, 차와 같으면 내접, 차와 합 사이면 두 점에서 만나고, 합과 같으면 외접, 합보다 크면 외부에 있다. 아래 그림을 보자.
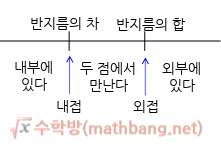
아 덕분에 조금 이해 되는듯...
중심선, 중심거리, 공통현
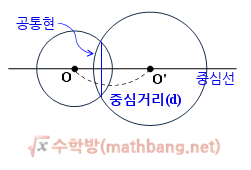
두 원의 중심 사이의 거리를 중심거리라고 한다고 했다.
이외에도 두 원의 위치관계에서 사용하는 용어에는 중심선과 공통현이라는게 있다.
중심선은 두 원의 중심을 연결한 직선이다.
공통현은 두 원이 두 점에서 만날 때에만 생긴다. 원과 부채꼴, 호, 현, 활꼴, 중심각에서 현은 원에서 두 점을 연결한 직선이라고 했다.
두 원이 만나는 두 점을 연결하면 현잇 ㅐㅇ기는데 이 현은 두 원 양쪽 모두에 공통으로 들어있어서 공통현이라고 부른다.
여기서도 두 원이 한 점에서 만날 때 그 점을 접점이라고 한다. 주의할 건 접점은 한 점에서 만날 때(내접, 외접)만 사용하는 용어다.
두 점에서 만날 때는 접점이라는 용어를 사용하지 않는다.
중심선은 공통현을 수직이등분한다. 참고로 알아두면 문제 푸는데 도움이 된다.
반지름의 길이가 3cm, 5cm 인 두 원이 있다. 중심거리 d가 아래와 같을 때 두 원의 위치관계를 말하여라.
(1) d = 4cm
(2) d = 8cm
(3) d = 12cm
이 문제를 풀 때는 큰 원의 반지름과 작은 원의 반지름의 합과 차를 미리 구하자. 그리고 중심거리와 비교하면 쉽다.
r + r' = 3cm + 5cm = 8cm, r' - r = 5cm - 3cm = 2cm 이다.
(1) d = 4cm이면 2cm보다는 크고 8cm보다는 작다. 반지름의 차보다 크고 합보다 작을 때는 두 원이 두 점에서 만나는 경우다.
(2) d = 8cm이면 두 원의 반지름의 합과 같다. 합과 같으면 외접, 즉 한 점에서 만나는 경우다.
(3) d = 12cm이면 두 원의 반지름의 합보다 크다. 따라서 두 원은 외부에 있으면서 만나지 않는 경우가 된다.
'Study > 알고리즘 | 자료구조' 카테고리의 다른 글
| [알고리즘] 재귀 접근 방법이란? | 자기 자신을 호출하는 함수 재귀함수 (0) | 2021.04.06 |
|---|---|
| [알고리즘_문제] 백준 1003 | 피보나치 함수 (0) | 2021.03.30 |
| [알고리즘] 벨만-포드 알고리즘 Bellman-Ford Algorithm 개념 잡기 (0) | 2021.03.15 |
| [알고리즘] 왜 숫자는 0부터 세어야 될까? 프로그래밍 언어의 비밀 (1) | 2021.03.09 |
| [알고리즘] 알고리즘의 성능은 어떻게 표현할까? | 알고리즘 성능 정리 (0) | 2021.03.09 |