
벨만-포드 알고리즘은 Richard E. Bellman(리처드 E 벨먼)과 Lestor Ford Junior(래스터 포드 주니어)의 이름에서 따온 알고리즘이다. 벨먼은 알고리즘의 중요 분야인 동적 계획법을 고안한 사람이기도 하다.
이 알고리즘은 그래프의 최단 경로 문제를 해결하기 위한 알고리즘이다.
모든 간선에 대해 가중치를 계산, 갱신해가며 가중치가 변경되지 않을 때까지 처리를 반복한다.
이 알고리즘을 해석해보자.

위 그래프는 똑같이 벨만 포드 알고리즘의 모습이다. 이 것을 파헤쳐보고자 한다.

먼저 초기 비용 값이 각 포인트에 할당된다.

모서리 중 하나가 선택된다. 편의를 위해 A-B 모서리를 선택했다.
끝점에서 끝점까지의 각 순회 비용이 발생하고,
선택한 모서리에서 계산된다.
계산은 초기 포인트의 비용 + 비용이 발생된다. 0+9 = 9
정점 B보다도 A가 현재 가중치가 작으므로 정점 A에서 정점 B로 가는 경우를 먼저 게산한다.
정점 A의 가중치는 0이고 간선(A,B)의 가중치가 9이므로 정점 A에서 B로 가는 가중치는 0+9이므로 9가 된다.

※ 가중치가 큰 정점에서 작은 정점으로 향하는 경우는
간선의 가중치가 마이너스가 아닌 이상 변경될 일이 없다.
계산한 결과가 현재 값보다 작으면 가중치를 새로운 값으로 변경한다.
정점 B의 현재 값은 무한대로 9가 작다.
따라서 가중치를 9로 변경한다.
값이 변경된 경우에는 어느 정점에서 온 경로인지를 표시해 둔다.
계속해서 반대 방향인 정점 B에서 정점 A로 향하는 경우를 계산해 보자.
정점 B의 가중치가 9이므로 정점 B에서 정점 A로 가는 가중치는 9+9 = 18이 된다.
정점 A의 현재 값 0과 비교하면 현재 값이 작으므로 가중치를 변경하지 않는다.

같은 작업을 모든 간선에 제공한다.
간선의 순서는 임의이지만, 여기서는 더 왼쪽에 있는 간선부터 계산해 가도록 한다.
간선을 하나 선택하자.

가중치를 변경했다. 정점 C의 가중치가 2가 되었다.

같은 방식으로 또 다른 간선을 선택한다.

※ 여기에서는 정점 B의 가중치가 간선(B, C)에 의해 변경됐기 때문에 경로가 (A,B)에서 (B, C)로 변경된다.
따라서 (A, B)의 주황색이 사라지고 새롭게 (B, C)에 주황색이 표시된다.
가중치를 변경했다. 현시점에서는 정점 A에서 정점 B로 가는 경우,
정점 A에서 직접 가는 것보다 정점 C를 경유하는 것이 가중치가 작다는 것을 알 수 있다.
모든 간선에 대해 변경 작업을 진행해 간다.
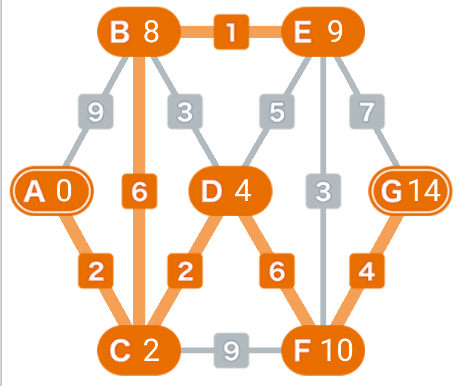
업데이트 작업이 없을 때까지 모든 모서리에서 반복된다.
더 많은 비용 업데이트가 발생한다.
간선 C-D와 C-F를 진행했다.
모든 간선에 대한 변경작업이 완료되었다.
이것으로 1라운드 작업이 끝났다. 같은 작업을 가중치가 변경되지 않을 때까지 반복한다.
2라운드 작업이 끝났다.

2라운듲 ㅏㄱ업이 끝났다. 정점 B의 가중치가 8에서 7로,
정점 E의 가중치가 9에서 7로 변경됐으므로 변경 작업을 한 라운드 더 실시한다.
3라운드 변경 작업을 진행했지만, 정점의 가중치가 변경되지 않았으므로 작업을 멈춘다.
이 시점에서 알고리즘에 의한 탐색이 완료되며, 시작점에서 모든 정점까지의 최단 경로가 나온다.

지금까지의 탐색에 의해 시작점 A에서 종점 G까지의 최단 경로는 A-C-D-F-G로
가중치의 합(간선의 가중치)이 14라는 것을 알 수 있다.
입력 그래프의 정점 수를 n 간선 수를 m이라고 할 때 계산 시간을 생각해보자.
벨먼-포드 알고리즘은 가중치 변경 작업을 n회 순회하면 마무리된다.
또한, 1라운드의 변경 작업에서는 각 간선을 1회씩 조사하므로 1라운드에 걸리는 계산 시간은 O(m)이 된다.
따라서 전체 계산 시간은 O(nm)이 된다.
설명을 간단히 하기 위해 앞의 그림에서는 비방향성 그래프를 사용했지만 방향성 그래프의 경우에도 최단 경로를 찾을 수 있다.
간선을 하나 선택해서 정점의 가중치를 계산할 때 비방향성 그래프에서는 A와 B의 간선처럼 양방향을 계산했지만, 방향성 그래프라면 간선이 향하는 방향으로만 계산할 수가 있다.
최단 경로를 구할 때는 보통 간선의 가중치는 시간이나 거리, 운임 등을 나타낸다.따라서 음수가 아닌 것이 일반적이다. 그러나, 벨먼-포드 알고리즘에서는 가중치가 음수라도 제대로 동작한다.단, 간선의 가중치의 합이 음수가 되는 폐로인 경우에는 그 폐로를 계속 순회하면 경로의 가중치를 작게 만들 수 있다.
즉, 애당초 최단 경로가 존재하지 않는다는 의미이다.
이때는 정점의 가중치 변경 작업을 n라운드 진행해도 정점의 가중치가 계속 변경되므로'최단 경로가 존재하지 않는다'는 판단을 할 수있다.
'Study > 알고리즘 | 자료구조' 카테고리의 다른 글
| [알고리즘_문제] 백준 1003 | 피보나치 함수 (0) | 2021.03.30 |
|---|---|
| [알고리즘_수학] 두 원의 위치관계, 내접, 외접 (0) | 2021.03.23 |
| [알고리즘] 왜 숫자는 0부터 세어야 될까? 프로그래밍 언어의 비밀 (1) | 2021.03.09 |
| [알고리즘] 알고리즘의 성능은 어떻게 표현할까? | 알고리즘 성능 정리 (0) | 2021.03.09 |
| [알고리즘] 알고리즘은 어떻게 학습할까? / 알고리즘 공부법 (0) | 2021.03.09 |

|

|

|
|

|